Le logiciel de service client omnicanal et 100% français
Pour moins de réclamations et plus de conversations !
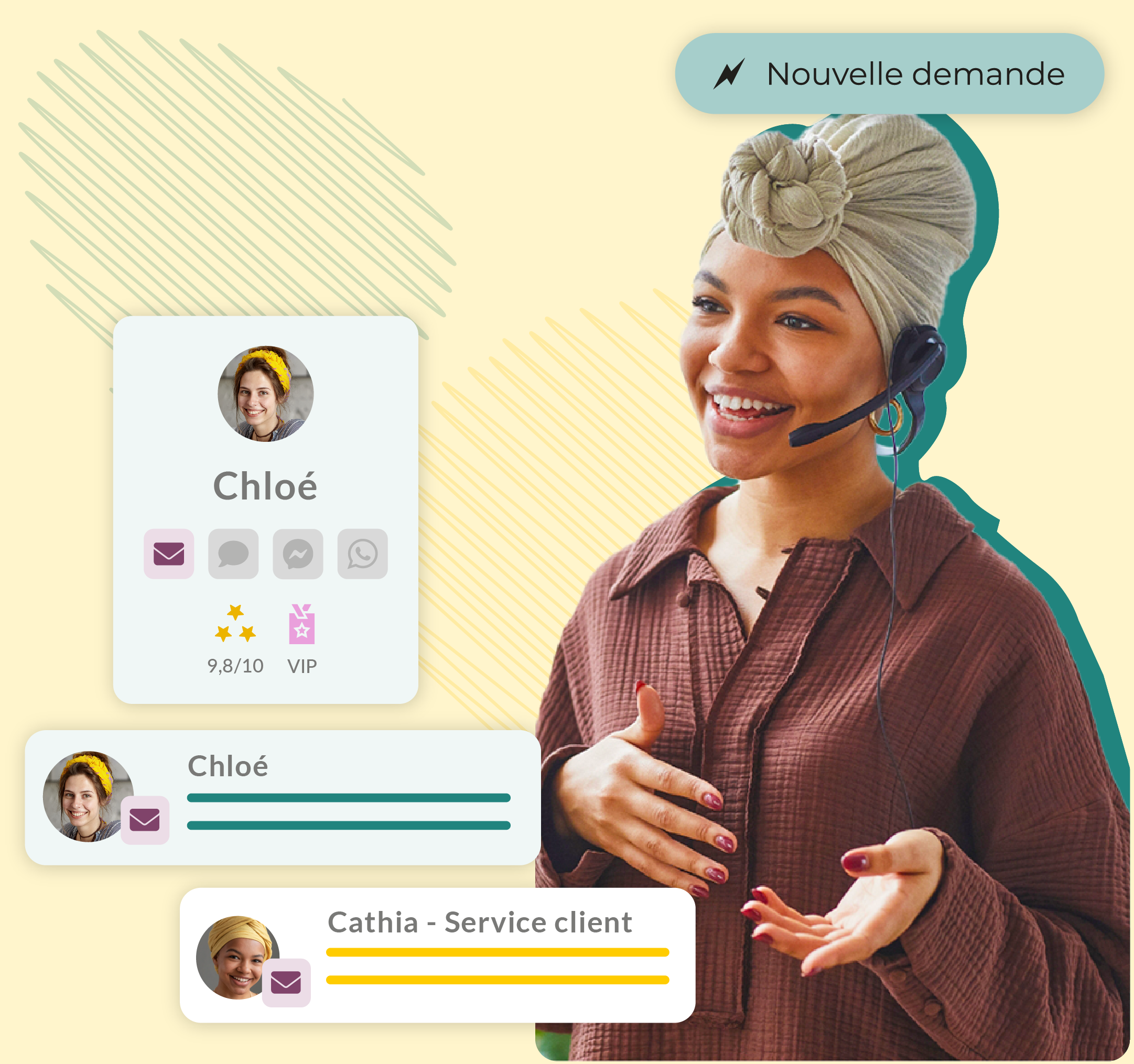
Une solution conçue pour vous simplifier la vie
Mettez en place la solution de service client qui vous ressemble : easiware s’adapte à tous vos besoins.
Intuitive
Profitez d’une interface pensée pour aider vos conseillers et faciliter leur quotidien.
Sécurisée
La sécurité est un enjeu clé : notre solution est conforme aux normes RGPD et certifiée HDS.
Made in France
De l’hébergement des données au support client : toute la chaîne de valeur est en France.
Flexible et sur-mesure
Une offre 100% sur mesure qui s’adapte au rythme de votre activité.
Gérer votre relation client n’a jamais été aussi simple
Plus de fonctionnalités, pour plus de flexibilité.
Centralisez tous vos canaux de communication
Bénéficiez d’une seule interface pour l’ensemble des canaux de communication de votre service client. Résultat : moins d’outils à mettre en place, moins d’onglets ouverts et aucune demande non traitée.
Apprenez à connaître vos clients
Bénéficiez d’une vision 360° de vos données clients sur une fiche personnalisée afin de proposer à vos clients une réponse rapide et adaptée, en prenant en compte leurs profils et l’historique des échanges.
Personnalisez votre relation client, sans les tâches répétitives
Définissez vos propres règles de gestion pour permettre à vos conseillers de se concentrer sur les tâches à forte valeur ajoutée et mieux travailler en équipe pour un suivi client optimal. Uniformisez vos communications avec des modèles de réponses.
Pilotez et anticipez votre activité
Mesurez l’ensemble de votre activité grâce à des tableaux de bords personnalisés avec les KPIs qui sont essentiels pour vous : DMT, volumétrie des demandes, productivité de vos conseillers, motifs de contacts de vos clients, etc… Toute la gestion de votre service client se mesure en temps réel.
Connectez vos outils métier à easiware
Simplifiez votre quotidien en centralisant l’ensemble de vos outils et données clients au sein de notre logiciel de service client.
Pour nous aussi, la relation client est primordiale
Plus qu’un outil, un projet commun
Travaillez main dans la main avec votre interlocuteur dédié qui vous aidera à construire une plateforme adaptée à vos besoins et qui continuera à vous accompagner après le lancement avec des recommandations stratégiques.
Une équipe support ultra-réactive
Profitez pleinement de la solution easiware avec une équipe de conseillers localisée en France. Ils sont disponibles pour vous aider au quotidien à utiliser l’outil à sa pleine puissance.
Des formations pour toujours progresser
Améliorez sans cesse la performance de votre équipe grâce à des formations personnalisées et certifiées Qualiopi. Notre catalogue de formation évolue en fonction de vos besoins.
Prêt à mieux répondre à vos clients ?
Notre équipe vous présente la solution en moins de 30 minutes.










